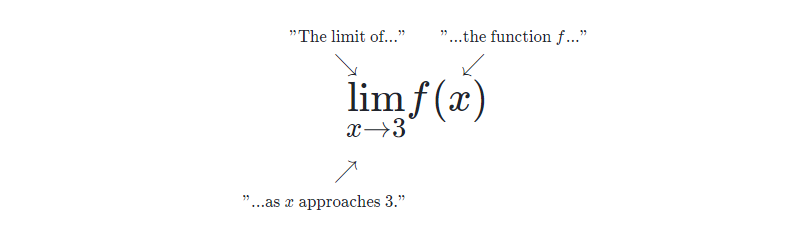극한
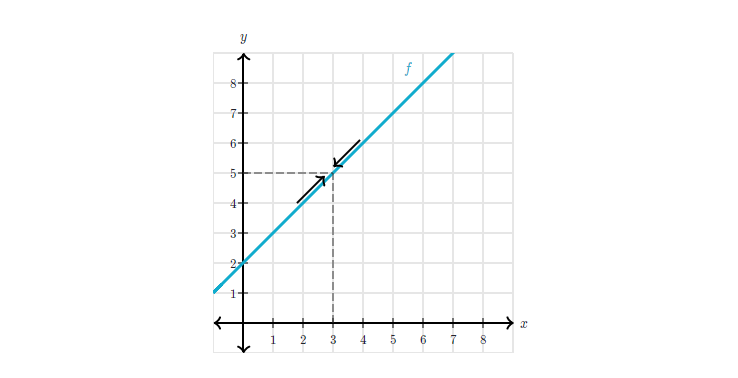
는 3일 때 의 극한은 함수의 결과 값 가 3일때의 값에 근접하여간다. 예를 들어 좌표에서 시작하여 가 3에 가깝게 움직일때마다 의 값은 5에 가까워지는 것을 확인할 수 있다.
유사하게도 좌표에서 시작하여 에 가깝게 왼쪽 아래로 움직여 본다면 의 값은 5에 가까워지는 것을 확인할 수 있다. 이러한 이유에서 가 3일때 함수 의 극한은 5라고 말할 수 있게 된다.
그렇다면 가 3일때 함수 의 극한과 가 3일때 함수의 값에 대한 차이에 대해 의문이 들 수도 있다. ex) 가 3일때 함수 의 극한과 의 값은 동일하다. 그러나 모든 경우에 대해서 성립하지는 않는다.
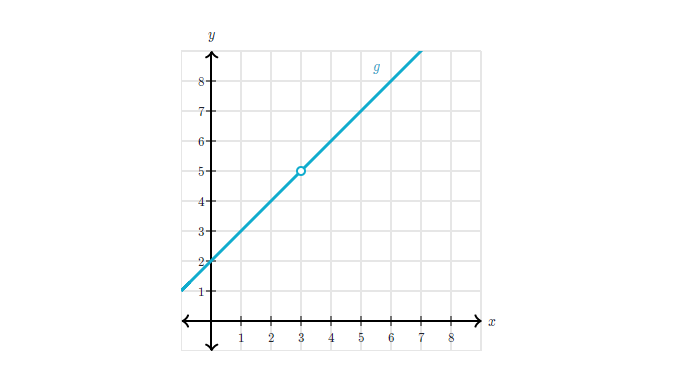
이것을 이해하기 위해서는 함수 를 보아야한다. 이 함수는 이 정의되지 않았다는 점만 제외한다면 와 동일하다.
함수 와 같이 함수 의 가 3일때 극한은 5이다. 일때 함수의 값은 5에 매우 가까워지는 것을 확인할 수 있기 때문이다. 그래서 일때 함수 의 극한은 5와 동일하다. 그러나 에서 함수 의 값은 정의되지 않은 상태이다. 그러므로 이들은 다르다.
이것이 극한의 아름다움이자 장점이다. 극한에서는 함수의 값이 실존하는 지에 대해서 의존하지 않는다. 그렇기에 함수가 극한에 가까워질 때 어떻게 동작하는지 설명할 수 있게 된다.
극한에 대해서 설명할 수 있는 또 다른 표기법도 존재한다. 아래의 예시는 함수 에서 에 근접한 극한 값을 나타낸다.
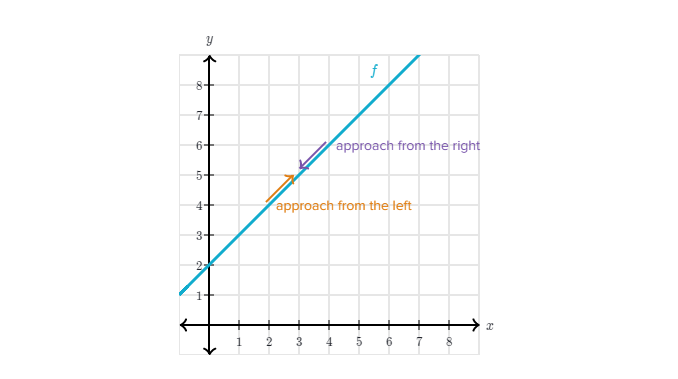
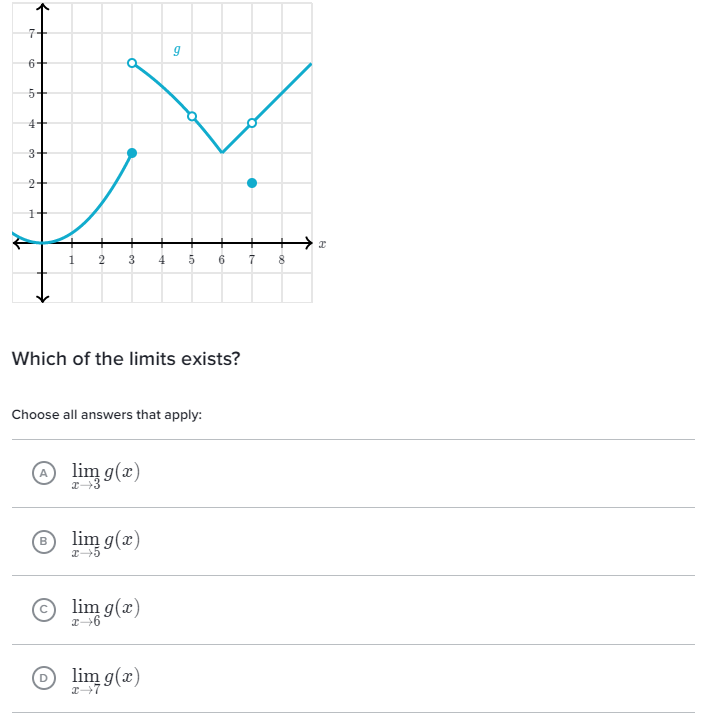
극한은 양쪽에서 동일해야한다.
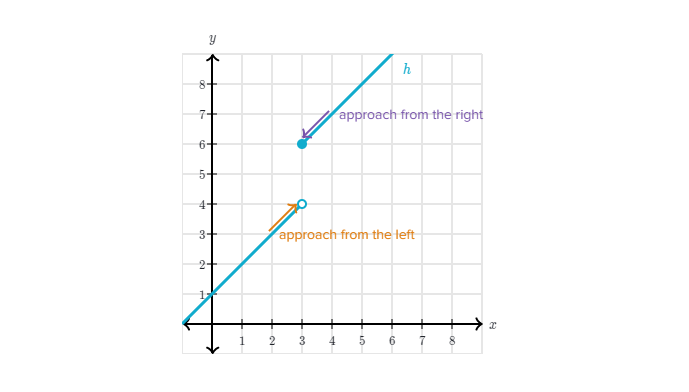
와 인 의 극한 값으로 돌아와보자. 우리는 의 값이 3을 향해 증가하던가 3을 향해 감소하는 것을 통해 5에 근접하는 방식을 볼 수 있다.
함수 를 예를 들어보자. 값은 의 값에 대해 오른쪽에서 접근하느냐 왼쪽에서 접근하느냐에 따라 달라진다. 에 대해 왼쪽에서부터 접근할때 함수는 4에 근접한다. 오른쪽에서부터 에 대해 접근하게 되면 함수는 6에 근접한다.
극한이 양쪽에서 동일한 값에 대해 접근하지 않는다면, 이때 극한은 존재하지 않는다고 한다.